What is a Concussion?
Until somewhat recently, concussions were seen as a relatively mild injury. However, in the last few years, a growing body of evidence has demonstrated the long-term consequences of these injuries to medical professionals and the public at large. Simply put, a concussion is a form of traumatic brain injury (TBI) caused by impact with the head [1,2,3, 4]. In the short term, symptoms can include disorientation, headache, memory loss, loss of consciousness, an inability to focus, tiredness, lack of coordination, nausea, and dizziness [1,2]. However, high-profile incidents involving former professional athletes combined with a substantial number of veterans returning from Operation Enduring Freedom and/or Operation Iraqi Freedom who have received head injuries has shown that concussions can result in serious long-term consequences including loss of cognitive abilities, depression, aggression, a loss of impulse control, anxiety, post-traumatic stress disorder, and premature death [1,3].
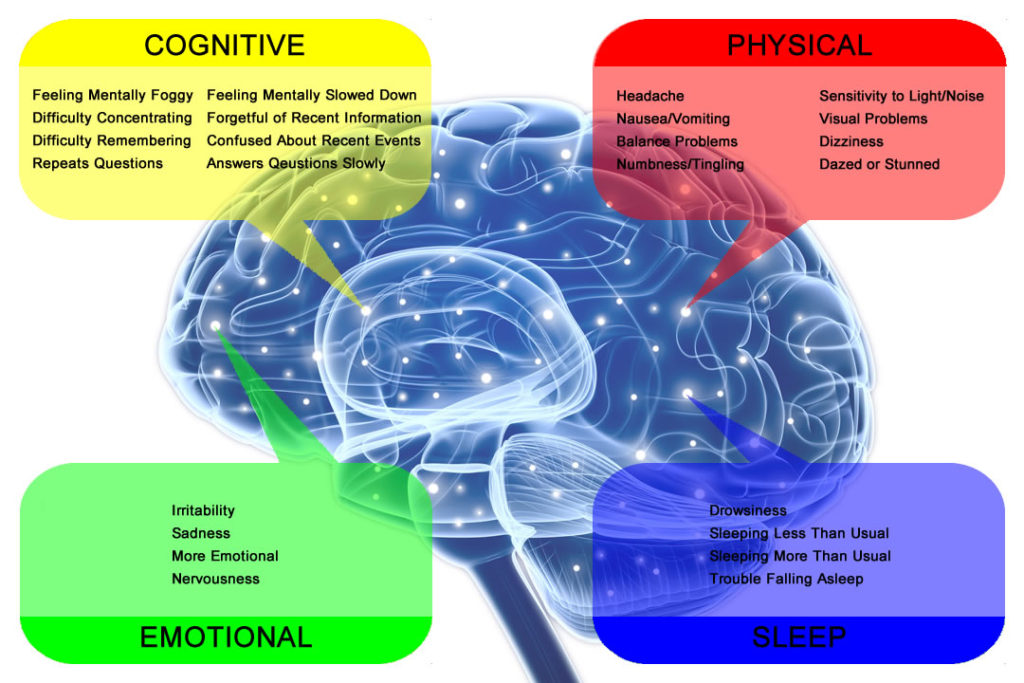
Symptoms of Concussions:
Concussion Symptoms [Online image]. Retrieved May 5, 2016 from http://www.advancedvisiontherapycenter.com/services/sports_vision/concussion_management/.
What activities cause concussions?
Concussions can occur as a result of many different types of activities. For veterans of recent military operations in Iraq and Afghanistan, concussions typically occurred due to explosive devices, gunshot wounds (with and without helmet penetration), and vehicle accidents. Vehicle accidents are also a common cause of concussions [5] for people living their day-to-day lives along with falling and physical assault [1]. Various sports such as football, soccer, hockey, etc can also lead to concussions. In these cases, concussions typically result from impacts with other players or from impacts with the ground [2,3,4]. SCA fencing shares these risk factors for concussions, particularly when we consider participation in melees. Fighters are also at risk for receiving concussions due to sword blows, which is the type of concussions that we will primarily focus on here.
Regardless of the activities that caused the impact, concussions typically occur in one of three ways:
Direct Impact with the Brain: This type of injury involves either the penetration of the skull by a foreign object or an injury that crushes the skull.
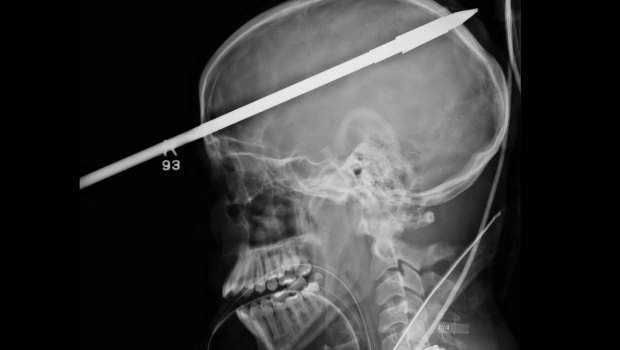
Yes, this would also cause a concussion: direct impact with the brain
Spear in Brain [Online Image]. Retrieved May 5, 2016 from http://brainandspine.titololawoffice.com/2012/07/articles/traumatic-brain-injury-tbi/phineas-gage-and-yasser-lopez-offer-modern-brain-injury-research-more-data/.
Linear Acceleration of the head: Acceleration of the head through space can cause the brain to impact the inside of the skull.
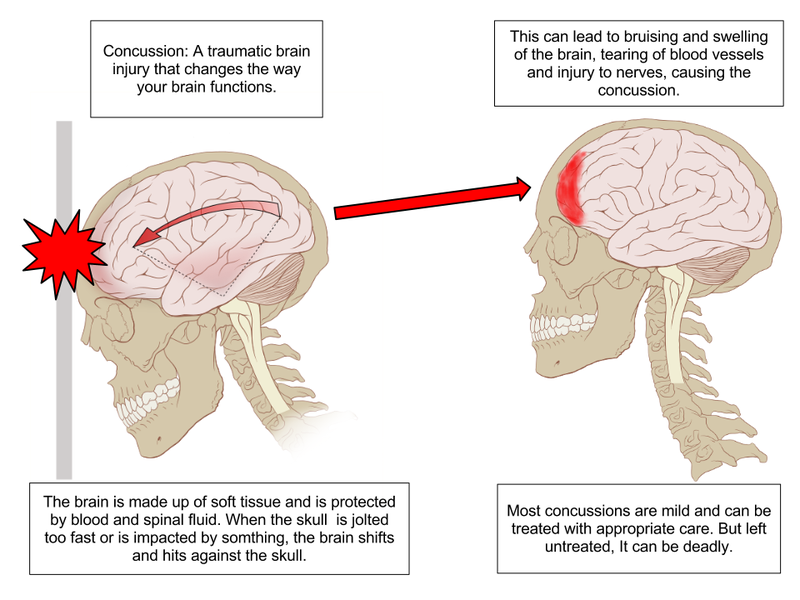
Linear acceleration causes the brain to impact the inside of the skull:
Andrews, M. (2012). Concussion Anatomy [Online image]. Retrieved May 5, 2016 from https://commons.wikimedia.org/wiki/File:Concussion_Anatomy.png.
Rotational Acceleration of the head: Rotation of the head on its axis can create shearing forces inside the brain that cut through neurons causing something called “diffuse axonal damage.” Indeed, rotational injury seems to be most responsible for sports injuries [6].
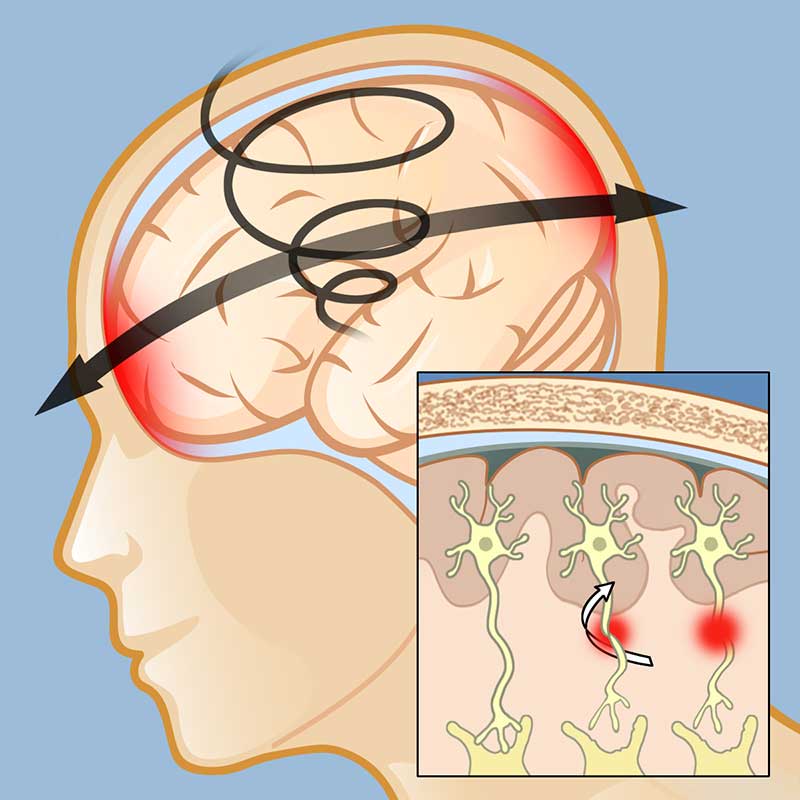
Concussion due to rotational acceleration leads to shearing of neurons in the brain.
Graves, T. (2014). Concussion [Online image]. Retrieved May 5, 2016 from http://weillcornellbrainandspine.org/condition/concussion.
Given that our blunted weapons should, in no way result in penetration of the skull, we can limit our discussion to concussions caused by either linear or rotational acceleration. The obvious next question is: How much acceleration is necessary to cause a concussion?
Unfortunately determining a clear threshold for injury is tricky. A recent study has shown concussions occurring from football impacts ranging from 60G – 168G (1G = acceleration due to gravity = 9.8 m/s2) [4]. However it is also clear that it is possible to undergo far greater acceleration without sustaining a concussion. For our purposes, it is sufficient for us to use a value on the lower end of this range in order to determine where concussions will start to occur, which gives us a value ~ 60G. However, there is some evidence that lower levels of impact (30G) may be sufficient to cause significant brain damage [5], so keep in mind that this threshold is currently a contentious aspect of concussion literature and is subject to changing due to new research.
How much force is required to accelerate the head 60 Gs?
While calculating the exact level of force is somewhat more complicated, the movement and acceleration of objects can be estimated rather simply using Newton’s First and Second Laws of Motion [7]:
- An object either remains at rest or continues to move at a constant velocity, unless acted upon by a force. (Inertia)
- The vector sum of the forces F on an object is equal to the mass m of that object multiplied by the acceleration vector a of the object: F = ma.
Linear Acceleration:
In other words, if we want to calculate how much force is needed to cause an object to accelerate a given amount, we will need to know its mass. A human head has a mass of approximately 5 kg and a fencing mask has a mass of approximately 2 kg, so for this calculation, let us assume a mass of 7 kg. First let us convert Gs of acceleration to the more typical metric unit, meters(m)/second(s)²:
A = 60G * 9.8m/s²/G = 588 m/s²
Then in order to calculate the necessary force to cause 588m/s² of linear acceleration, we get:
F = 7kg * 588 m/s² = 4116 kg*m/s²
In the metric system, the unit for force is the Newton (N), which is equal to 1 kg*m/s², so the necessary force to cause this level of linear acceleration is 4116 N. However, I expect that most people reading this series of articles are located in the US and so Newtons aren’t a particularly intuitive unit of measurement. Fortunately the unit for force in the US/Imperial system of measurements is the pound and the conversion factor between these measurements is 4.45 N = 1 lb. We then have:
4116 N = 925 lbs
Rotational Acceleration:
Calculating the necessary force required to cause this level of rotational acceleration is slightly more complicated. Rotational force is calculated using a slightly different equation, so rather than using F = M * A, we instead calculate for torque:
torque(τ) =moment of inertia( I) * angular acceleration(α)
Since we have already converted from Gs to m/s2, we must now calculate the moment of Inertia. The equation for this is as follows:
I = constant (k) * mass (m) * radius (r)²
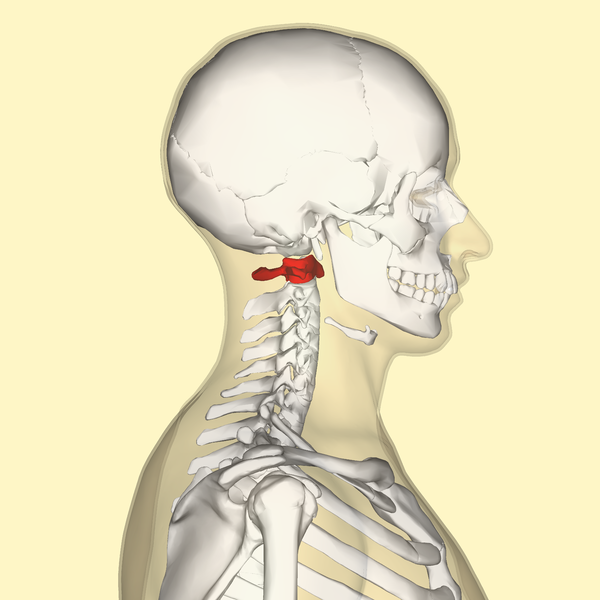
Location of the atlas (shown in red) and axis (immediately below and encapsulated by the atlas). These bones form the joints that allow the head to rotate.
Anatomography. (2012). Atlas [Online image]. Retrieved May 5, 2016 from https://commons.wikimedia.org/wiki/File:C1_lateral.png.
So now, in addition to knowing the mass of the head, we must also know its radius. Anatomically the head rotates vertically (nodding) in the joint between the occipital bone of the skull and the atlas bone and horizontally (side-to-side) in the joint between the atlas bone and the axis bone (the atlas is shown in red above and the axis is mostly obstructed by the atlas, but is visible as a small sliver of white under the atlas). Knowing this, we can measure from this point to the chin of a fencing mask, which is around 10 cm. We can therefore calculate I as follows:
I = k * 7kg * 0.1 m² = k * 7 * 0.01 m = k * 0.07 kg*m²
You will note that this leaves the term, k which I have not yet defined. In this equation, k is a constant term that is dependent on the shape of the object being rotated. Choosing an appropriate k-value is complicated, so let us come back to it. For now, let k = 1. We can then finish calculating the necessary force to cause this kind of rotational acceleration:
τ = 0.07 kgm²*588m/s² = 41.16 N*m
In this case, the “meters” part of the result is related to the radius, so we can get rid of it as follows:
41.16 N*m / 0.1 m (the radius) = 411.6 N = 92.5 lbs
Choosing a value for k
Calculating a precise value for k is tricky because the head, particularly a head encased in a fencing mask is strangely shaped, the axis of rotation is off-center, and the mass is not uniformly distributed, however we can estimate a value for k by selecting a geometric shape that is similar to the shape of the head and using its k value here. That is, As the old physics joke goes, assume a spherical head. In this case, the value for k is 0.4. So, taking that into consideration, we would then multiply our result by this value:
411.6 N * 0.4 = 164.64 N = 37 lbs
Given that we’re “fudging” the shape of the head here, we should take this value with a grain of salt and understand that the correct value should lie somewhere between these two values. In other words, the needed force is somewhere between 164.64 N – 411.6 N or in Imperial measure, 37 lbs – 93 lbs.
Editing Note: These calculations will be addressed again in article 5 to use experimentally-derived values for moment of inertia.
Conclusion:
From the perspective of our combat sport, rotational acceleration poses the greatest risk for concussions, which is consistent with research into concussions in other sports. Importantly, the level of force needed to cause a concussion due to rotation is relatively low. In the next article, we will compare these levels to the measurements of striking force carried out by Baron Llwyd.
Works Cited:
- Centers for Disease Control and Prevention. (2015). Report to Congress on Traumatic Brain Injury in the United States: Epidemiology and Rehabilitation. National Center for Injury Prevention and Control; Division of Unintentional Injury Prevention. Atlanta, GA. http://www.cdc.gov/traumaticbraininjury/pdf/tbi_report_to_congress_epi_and_rehab-a.pdf
- McCrea M, Guskiewicz KM, Marshall SW, et al. Acute Effects and Recovery Time Following Concussion in Collegiate Football Players: The NCAA Concussion Study.JAMA. 2003;290(19):2556-2563. doi:10.1001/jama.290.19.2556.
- Guskiewicz KM, McCrea M, Marshall SW, et al. Cumulative Effects Associated With Recurrent Concussion in Collegiate Football Players: The NCAA Concussion Study.JAMA. 2003;290(19):2549-2555. doi:10.1001/jama.290.19.2549.
- Guskiewicz KM, Mihalik JP, Shankar V, et al. (2007). “Measurement of head impacts in collegiate football players: Relationship between head impact biomechanics and acute clinical outcome after concussion”. Neurosurgery 61 (6): 1244–52; discussion 1252–3.doi:10.1227/01.neu.0000306103.68635.1a.
- Varney NR, Roberts RJ. Forces and accelerations in car accidents and resultant brain injuries. In: Varney RN, Roberts RJ, editors. The Evaluation and Treatment of Mild Traumatic Brain Injury. Mahwah, NJ: L Erlbaum; 1999. pp. 39–47.
- R.C. Cantu. Guidelines for return to contact sport after a cerebral concussion. Phys Sports Med, 14 (1986), pp. 75–83
- Barth, J. T., Freeman, J. R., Broshek, D. K., & Varney, R. N. (2001). Acceleration-Deceleration Sport-Related Concussion: The Gravity of It All. Journal of Athletic Training, 36(3), 253–256.
Pingback: Ruairc
Pingback: Simon
Pingback: Toki Ima
Pingback: Indy
Pingback: Concussions in Fencing part 2: The Typical Blow « The Weekly Warfare
Pingback: Concussions in Fencing Part 3: Other Factors « The Weekly Warfare
Pingback: Concussions in Fencing Part 4: Techniques for Avoiding Concussions « The Weekly Warfare
Pingback: Concussions in Fencing 5: Armoring Up « The Weekly Warfare